There are numerous ways to assess an electoral system. Mathematicians and political scientists have developed hundreds of different criteria, with the most common including the majority criterion, the later-no-harm criterion and the Condorcet winner criterion.

The Condorcet winner criterion is one of the most common criteria. It states that the candidate who would win a one-on-one matchup against any other candidate should win the election. The frequency with which an electoral system elects Condorcet winners is a good measure of whether the election system reflects the political center of a given electorate, since a Condorcet winner, by definition, has to be able to win over a majority of the electorate regardless of alternative choices.

A system that more often elects Condorcet winners will less often elect a candidate disliked by the majority of voters--an outcome that US voters in plurality elections and low turnout runoffs know all too well. It is hard to estimate how many US elections using plurality and runoff systems elect candidates disliked by a majority of voters, but we all have anecdotes of reviled politicians who somehow manage to keep being re-elected.

Ranked choice voting (RCV), on the other hand, tends to elect Condorcet winners. San Francisco started using ranked choice voting in 2004. Since then, four Bay Area cities have held 138 elections for the 53 offices elected in those cities. Of these 138 winners, 46 did not win a majority of the first round votes, and 17 either trailed in first choices or led by less than five percentage points in the tally of first choices. Yet in every single instance, the winner of the election has been the candidate who would defeat all others in a head-to-head contest -- that is, “the Condorcet winner.” This includes seven races where the candidate with the most first choice rankings -- the likely plurality voting winner -- was defeated.

It is possible to study the Condorcet winner criterion in RCV elections (but not plurality or majority runoff elections) in the United States for two reasons. First, an RCV ballot, in which voters rank candidates in order of preference, carries far more information about voter preferences than a traditional plurality ballot in which voters merely choose one candidate. Second, the two California counties where RCV elections are held publish “ballot image” data online. Ballot image data is the record of how each voter ranked the candidates with all identifying information about the voter removed.  We can use this ballot image data composed of the compiled preferences of the electorate to simulate how the election would have gone if, say, one candidate had dropped out of the race, or another candidate had made it into the final round of vote tallying. We can also use the data to test which candidate would have won in a one-on-one  matchup against every other candidate.

Here are three reasons that RCV elections have typically chosen Condorcet winners:

• Most single-winner elections, whether using plurality, majority runoff or RCV, are not very close. Of the 138 RCV races for which we have collected data, only 51% had runner ups that received two-thirds as many votes as the winner. In only 34% was the margin between the winner and the runner up in the first round less than 20 points, and only in 11% was the first round margin between the winner and the runner up less than 5 points.

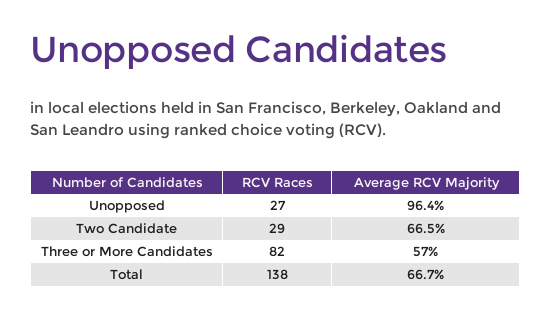
• Similarly, most local elections in the United States are low turnout and are held in localities with relatively uniform policy preferences (though local issues can still be extremely divisive). Because of the low stakes and (often) non-partisan nature of these elections, many local elections, whether held under plurality, runoff or RCV,  feature no more than two candidates, if they feature a second candidate at all. Incumbency advantages can be extremely powerful in local elections, and many races with two candidates were so skewed in favor of popular incumbents that one can see why they are often unopposed. In our dataset, 27 winners ran unopposed and 29 had a single opponent. In these cases the winner was technically the Condorcet winner, but the Condorcet criterion is more or less meaningless.

• Even in competitive elections, it is less likely that RCV will pick a non-Condorcet winner then some mathematicians suggest. RCV elections and Condorcet elections are both majoritarian, and there are simply not many situations where a majority of voters would choose one candidate over the runner up, but would choose a third candidate consistently over each of them. Our dataset contained only a few lower tier candidates who were stronger in one-on-one matchups against the winner than the runner up, and none of them would have beaten the winner.

There are critics of RCV who suggest that RCV will frequently elect non-Condorcet winners, but this data suggest this concern is overblown. Furthermore, if we assume that voters’ rankings reflect their sincere (rather than strategic) views on the candidates, our data show that a plurality system would have elected the non-Condorcet winner in 7 elections. In addition, under a runoff system, the Condorcet winner would have failed to reach the runoff in one instance and other Condorcet winners might have lost in runoffs that had smaller, less representative electorates. In other words, just as anticipated, RCV is more likely to elect a Condorcet winner than either plurality voting or runoff elections -- the only other single winner systems used in governmental elections anywhere in the world.

None of this is to suggest that political scientists and mathematicians are wrong to continue critically assessing voting methods and collective decision mechanisms. However, when it comes to implementation in the U.S., it is clear that ranked choice voting is not only the most achievable reform, but that it also succeeds where many of its critics claim it should not.

This blog post was originally posted at FairVote.org here.